CESE/DUAL-CESE

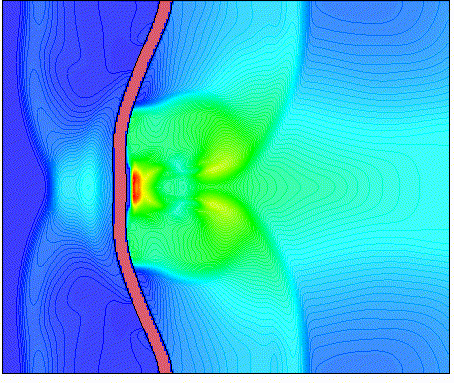
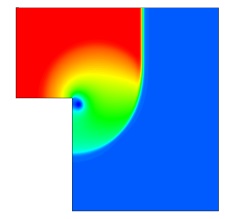
The folder provides input decks for the Conservation Element/Solution Element (CESE) solvers available in LS-DYNA. The CESE method is a novel numerical framework for conservation laws. It has many non-traditional features, including a unified treatment of space and time, the introduction of conservation element (CE) and solution element (SE), and a novel shock capturing strategy without using a Riemann solver. To date, this method has been used to solve many different types of flow problems, such as detonation waves, shock/acoustic wave interaction, cavitating flows, and chemical reaction flows. In LS-DYNA, it has been extended to also solve fluid-structure interaction problems with the embedded (or immersed) boundary approach or moving (or fitting) mesh approach.

DUAL-CESE

This folder contains examples using the DUALCESE solver. Compared to the regular CESE solver, the DUALCESE solver is more accurate and stable, particularly for coarse and triangle(2D)/tetrahedron (3D) meshes. It also features multiphase flow capabilities. Notes: multiphase capabilities have become available with the R13 release, while multiphase flow FSI is only available in R14 or more recent.

CESE

The *CESE keyword cards provide input for the legacy Conservation Element/Solution Element (CESE) solver. Users that have access to recent LS-DYNA versions are encouraged to transition to the *DUALCESE solver that offers more accuracy and stability over the classic *CESE approach. Features of the *CESE solver are progressively incorporated and expended upon in *DUALCESE.