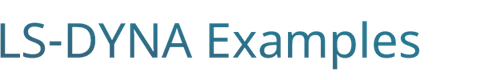EM

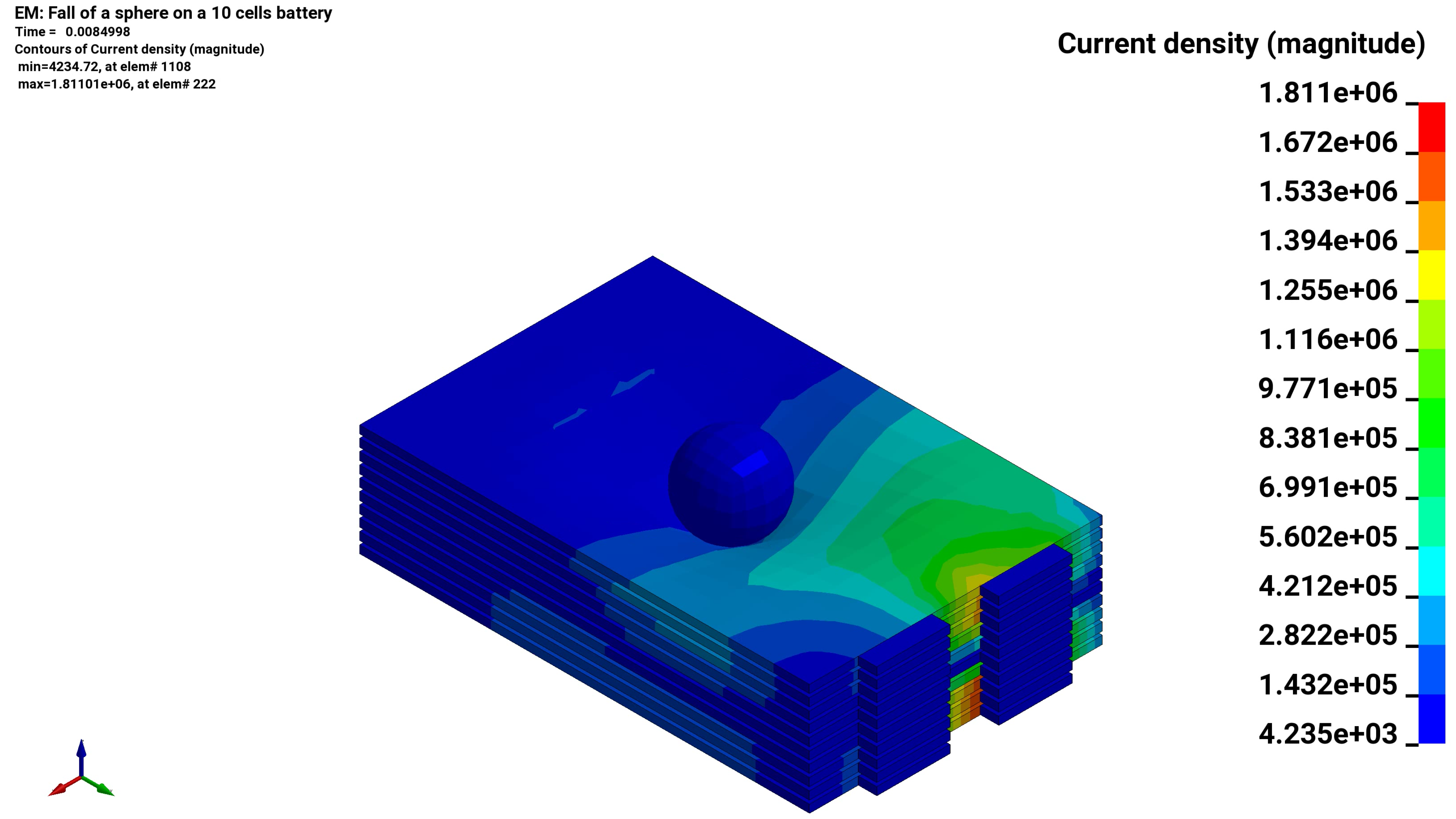
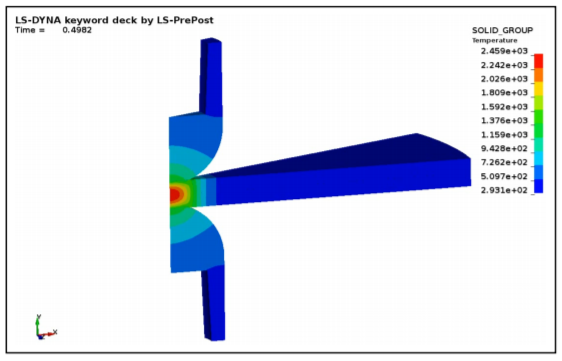
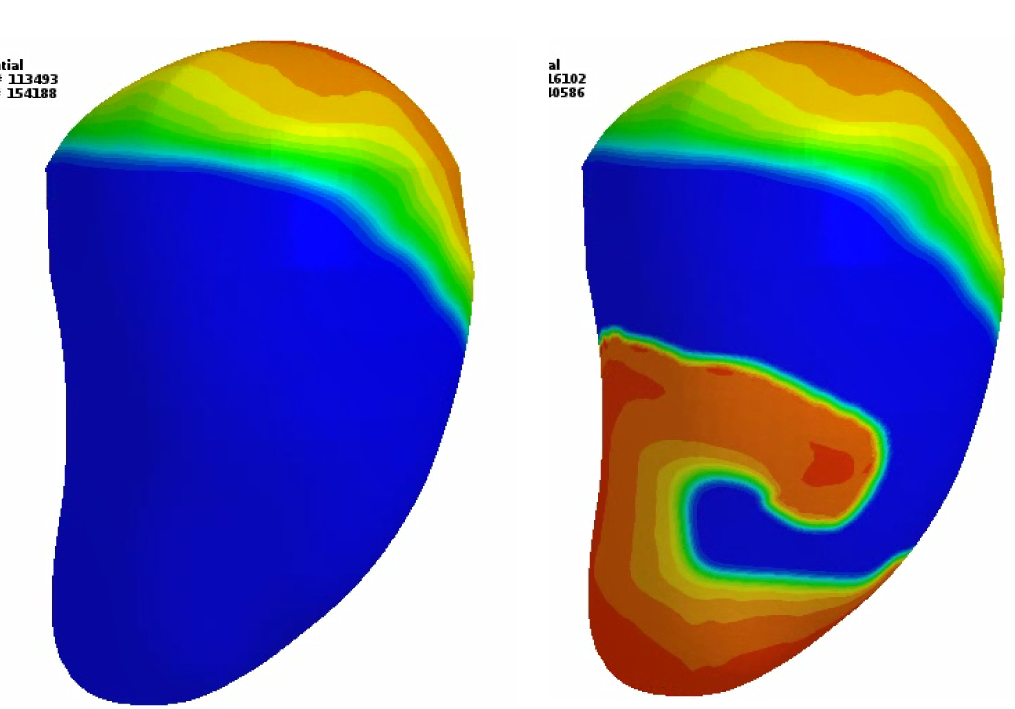
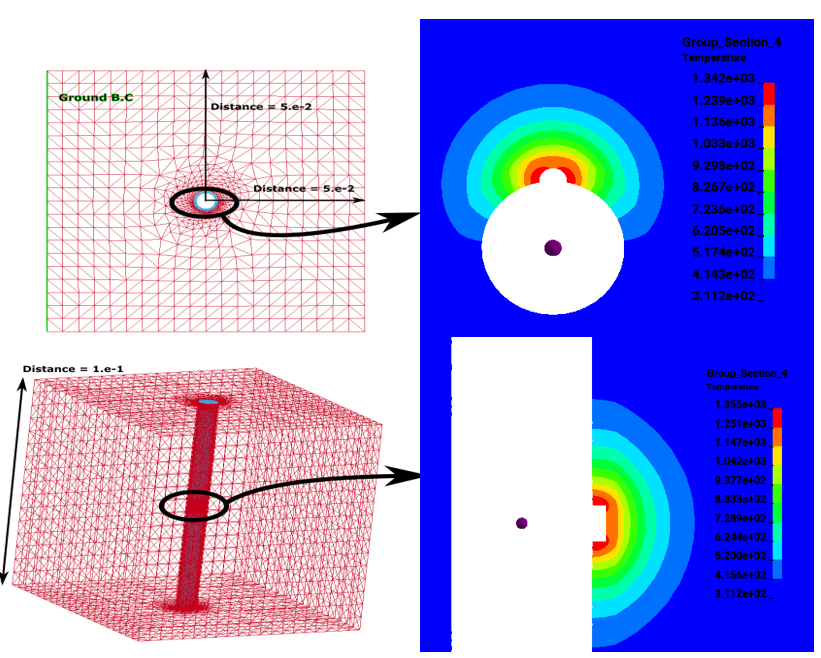
The *EM keyword cards provide input for a new electromagnetism module for solving 3D eddy-current, inductive heating or resistive heating problems, coupled with mechanical and thermal solvers. Typical applications include magnetic metal forming and welding. A boundary element method in the air is coupled to finite elements in the conductor in order to avoid meshing the air. For Eddy current related applications, you can follow this series of tutorial videos : https://www.youtube.com/watch?v=W4OBO6hZQak

Tutorial Resistive heating

This folder contains several input decks that aim to progressively introduce the user to the main keywords and concepts used by the EM resistive heating solver. Some of the features are only available for LS-DYNA R12 branch or in recent Development versions so make sure to have the correct executable installed. The revision (SVN) number is always indicated in the header of the main input deck ('i.k') along with some other critical information pertaining to the specific input deck. See the Download section for more information.

Tutorial Battery modelling

This folder contains several input decks introducing the different ways of modelling battery charges and discharges by using the EM resistive heating solver as well as handling abuse scenarios that may trigger external or internal shorts. Some of the features are only available for LS-DYNA R12 branch or in recent Development versions so make sure to have the correct executable installed. The revision (SVN) number is always indicated in the header of the main input deck ('i.k') along with some other critical information pertaining to the specific input deck. See the Description and Download sections for more information.

Tutorial Resistance Spot Welding

This folder contains several input decks that focus on the resistance spot welding application (RSW). Some of the features are only available for LS-DYNA R12 branch or in recent Development versions so make sure to have the correct executable installed. The revision (SVN) number is always indicated in the header of the main input deck ('i.k' or 'main.k') along with some other critical information pertaining to the specific input deck. See the Download section for more information.

Tutorial Eddy Currents

This folder contains examples using the EM solver and Eddy Currents. Applications include Magnetic metal forming (EMF), pulse welding, tube expansion, coil shape optimization, inductive heating, railgun and more.

Tutorial Electrophysiology

The EM solver electrophysiology (EP) capabilities start with the simulation of the propagation of the cell transmembrane potential in the heart. In this directory, some benchmarking and validation cases are shown. Some of the features are only available for LS-DYNA R12 branch or in recent Development versions so make sure to have the correct executable installed. The revision (SVN) number is always indicated in the header of the main input deck ('i.k' or 'main'k) along with some other critical information pertaining to the specific input deck. See the Download section for more information.

Tutorial RadioFrequency (RF) heating

This folder contains several input decks that aim to showcase some Radiofrequency (RF) heating examples. In the context of the EM solver, radiofrequency heating can be viewed as an extension of the traditional Resistive heating solver. Contrary to resistive heating, the material’s electrical conductivity is usually very low, or the material can be an insulator, but the input source is in a high frequency range (GHz or higher) which triggers molecular displacements that generate heat via friction. This dielectric heat source term becomes the dominant factor rather than the Ohmic losses term. Some of the features are only available for LS-DYNA R15 branch or in recent Development versions so make sure to have the correct executable installed.