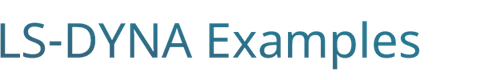Tutorial Eddy Currents
Basic Eddy current problem set up
This example shows the basic keywords mandatory in order to turn on the EM solver and set up a Eddy current problem. The current flows through the rod and an induced magnetic field is generated. The mesh has been set up based on the skin depth value to ensure enough refinement to capture the current diffusion though the thickness.
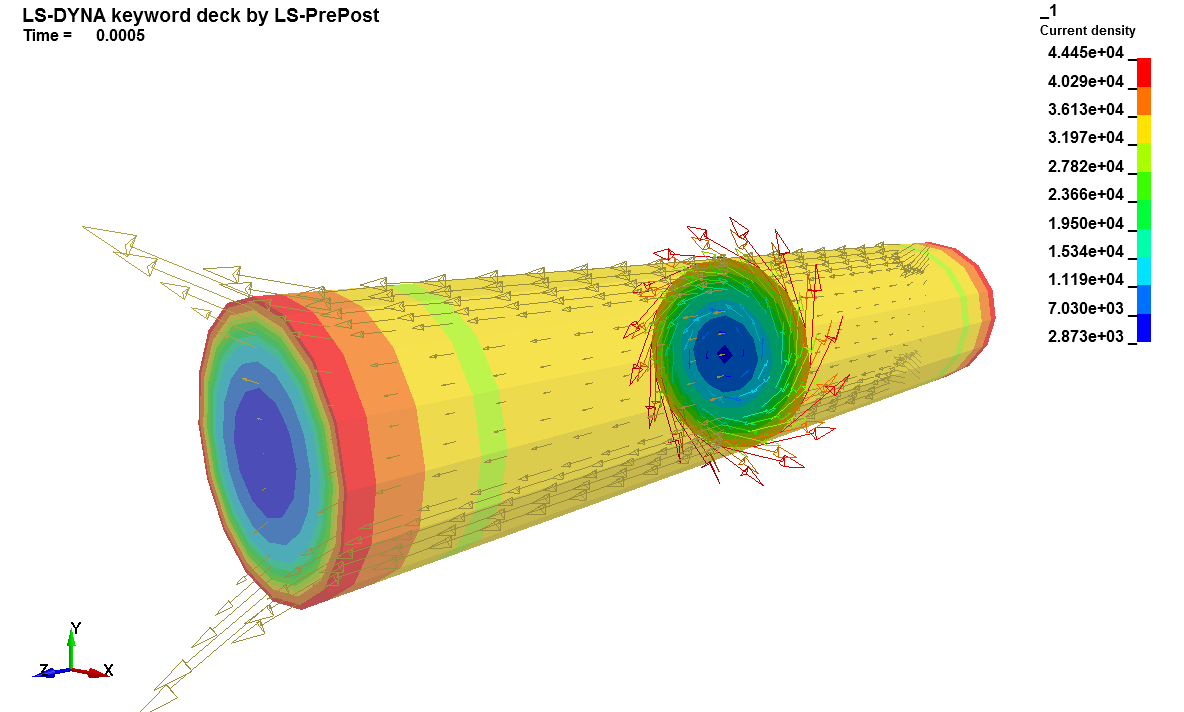
Electromagnetic forming problem
This LS-DYNA simulation shows a simple Electromagnetic forming example using the EM solver. A R,L,C circuit is defined in the coil which produces induced currents in the workpiece. This in turn generates Lorentz forces which cause the plate to move. Local heating is also produced and handled by the thermal solver.
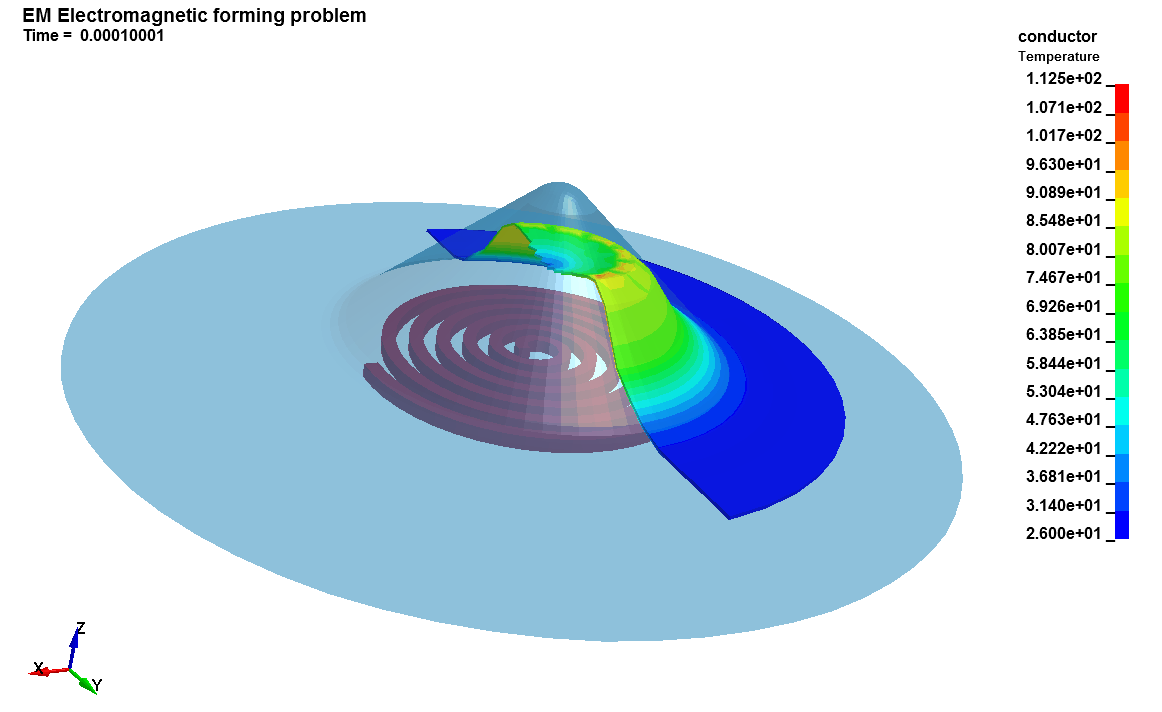
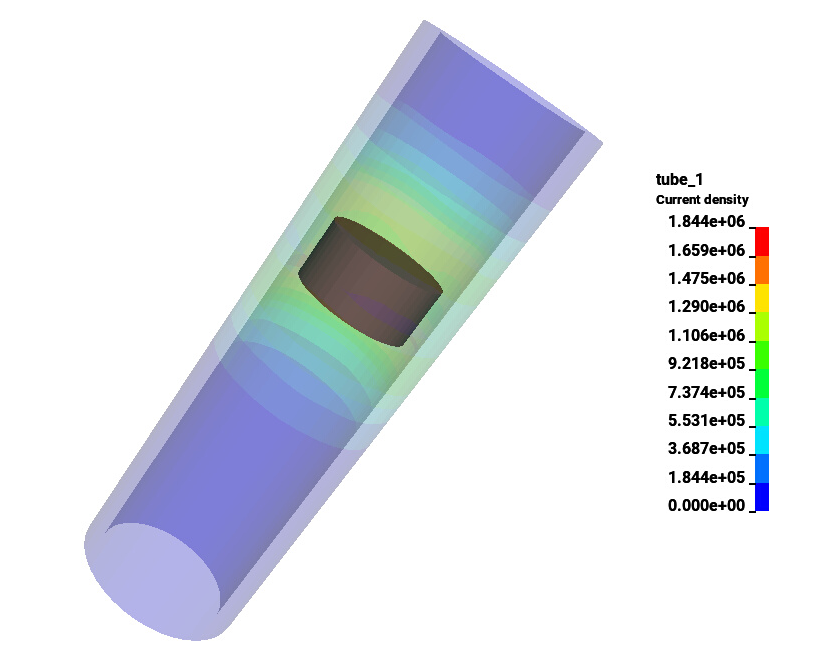
Tube expansion problem
This LS-DYNA simulation shows a simple Tube expansion example using the EM solver. A current is imposed in the coil which produces induced currents in the workpiece. This in turn generates Lorentz forces which cause the tube to expand. This problem is of medium size so running with 4 or more CPUs is recommended.
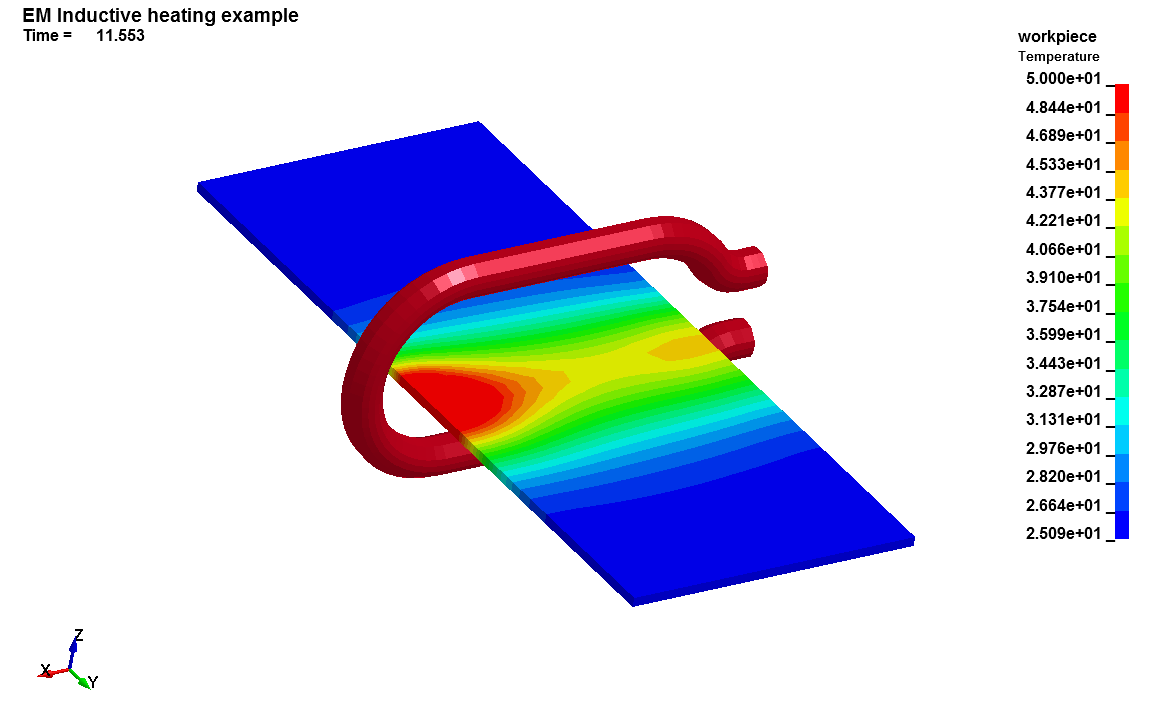
Inductive heating problem
This LS-DYNA simulation shows a simple inductive heating problem. A micro EM timestep is calculated using the circuit's current period divided by a factor NUMLS. Over a whole period, the full Eddy current problem is solved. An average Joule heating is calculated which is then given to the thermal solver over all the subsequent periods until reaching a time defined by a EM macro timestep.
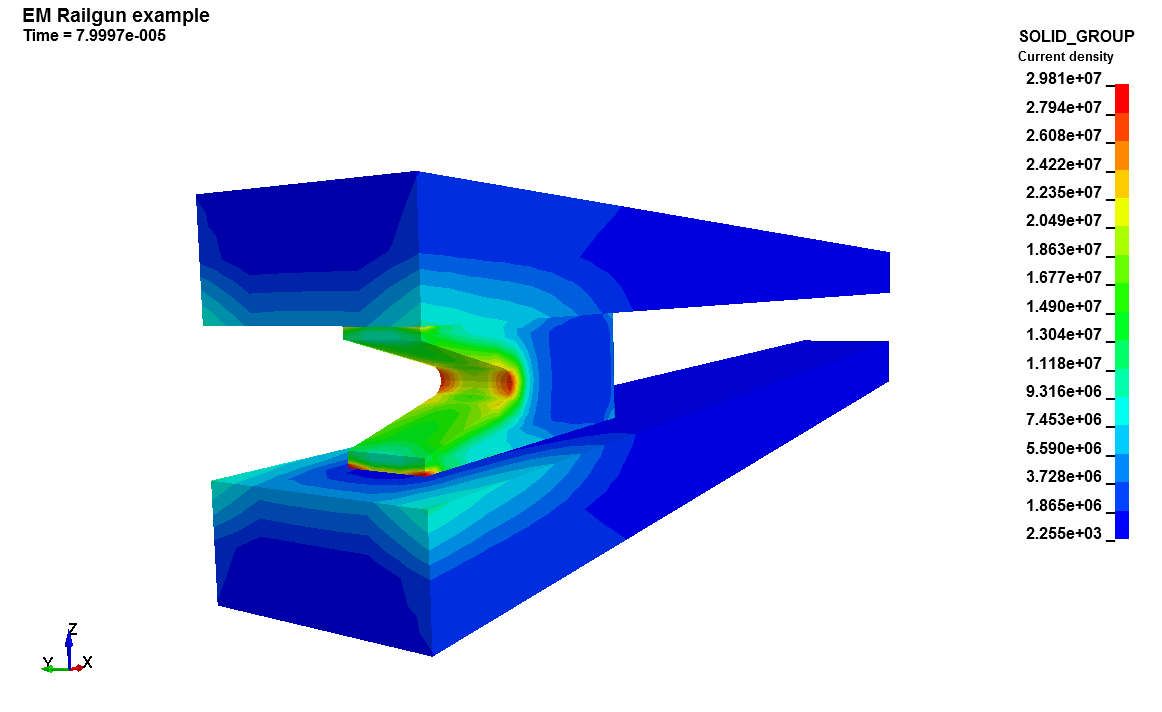
Railgun
A railgun consists of two parallel metal rails connected to an electric power supply. The projectile completes the circuit. The current flowing through the rails and projectile generates a magnetic field which in turn generates a Lorentz force propelling the projectile out of the barrel at a very high speed.
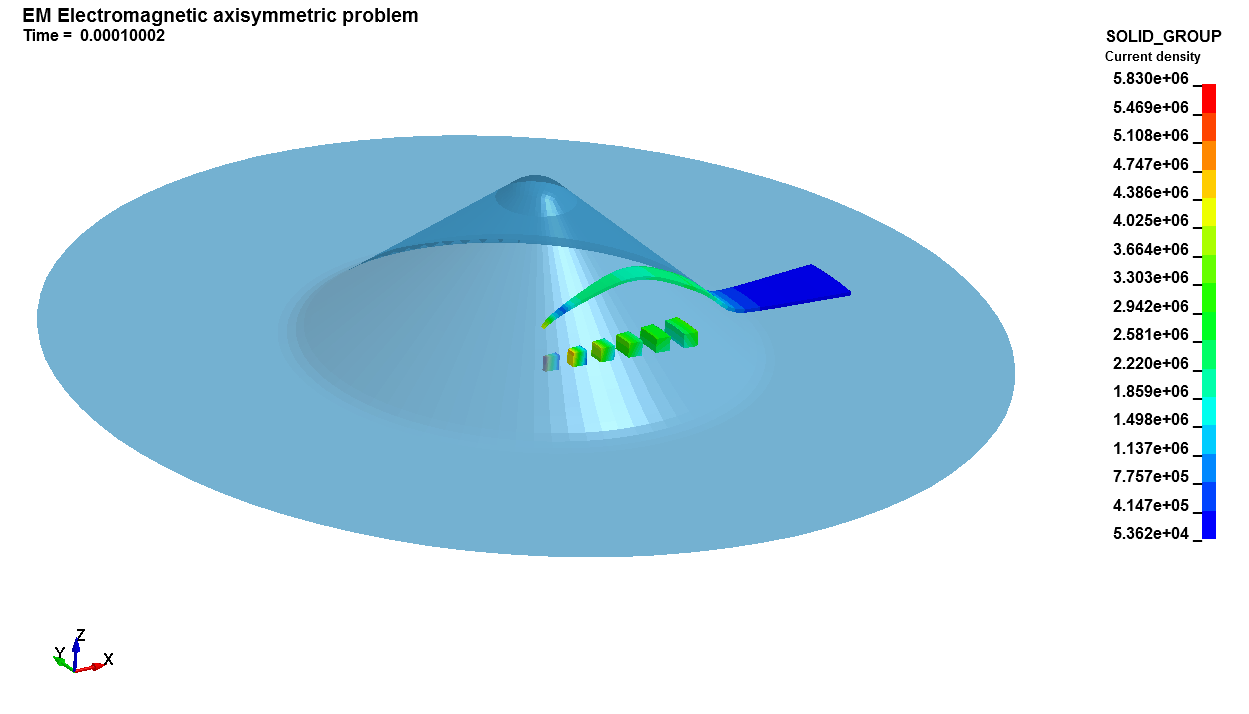
Axisymmetric problem
The R9 version introduced many new advanced capabilities to the axisymmetric solver. For example, it is now possible to simulate pancake or helicoid type of coils by connecting the different turns using EM_CIRCUIT_CONNECT therefore expanding the range of applicable EM forming or bending problems that can be solved using the axisymmetric solver.
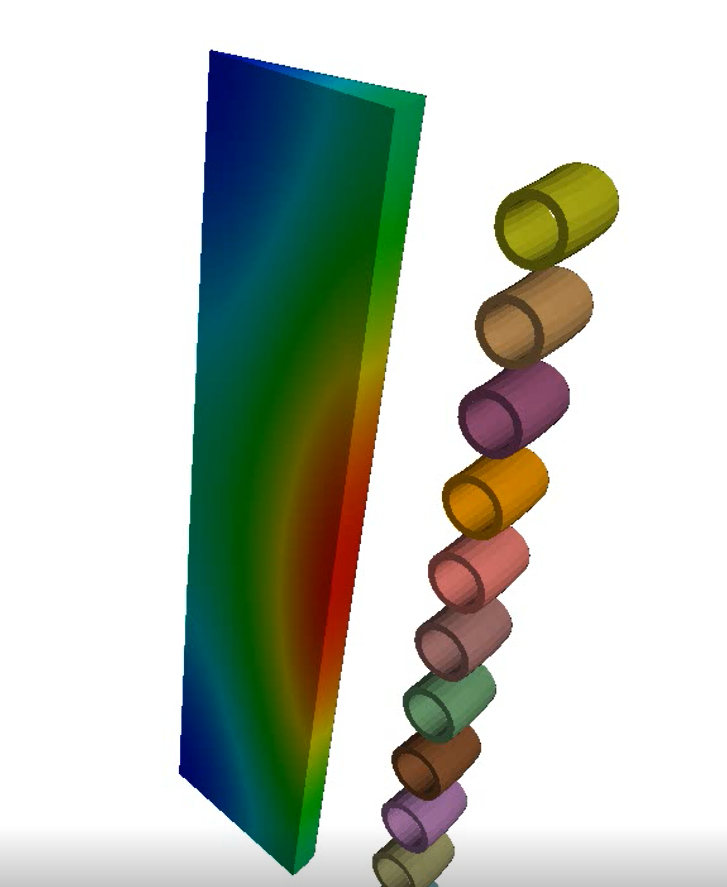
2D Axisymmetric Inductive heating
2D axisymmetric Inductive heating example with periodic recomputation of EM fields. This example uses the monolithic solver to solve the FEM/BEM system which allows to use higher timesteps (See choice of numls).

Coilgun
This example shows a coilgun simulation, also known as a Gauss rifle. It is a type of projectile accelerator consisting of one or more coils used as electromagnets in the configuration of a linear motor that accelerate a ferromagnetic or conducting projectile to high velocity. The EM solver is coupled to the Solid mechanics LS-DYNA solver.
Lenz's Law: Magnet Through a Copper Tube
Here, we reproduce an experiment from high school physics: a permanent magnet falls through a copper pipe. The temporal change of the magnetic field in the copper induces currents which themselves create an opposing magnetic field that brakes the fall. As a result, an equilibrium for the magnet's velocity can be reached. This phenomena is also known as Lenz's law.
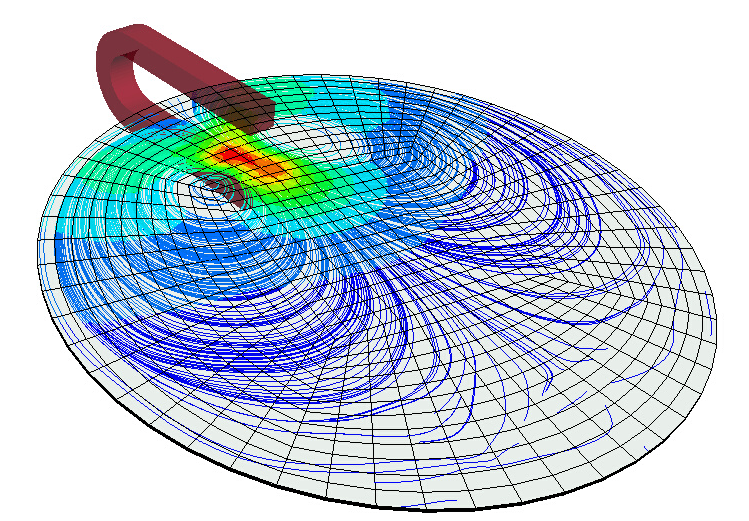
Arago's disk
A bar magnet is suspended above an aluminum disk. When the disk starts spinning, it will 'drag' the magnet and cause it to start spinning in the same direction albeit at a lower speed. The effect was discovered by François Arago in 1824. The method used here is a monolithic FEM-BEM approach available in the latest versions of LS-DYNA's EM solver.

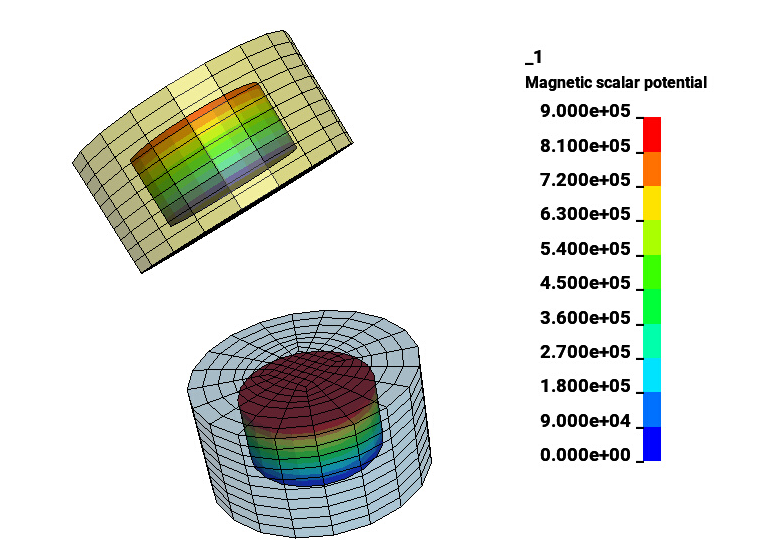
Laminate sheet closure using magnets
In this simulation, several magnets are embedded in a soft laminate structure. The objective is to study the latching of the two structure together, based on the positioning of the different magnets. It uses the FEM-BEM monolithic magnetostatics solver (used for zero-conductivity ferromagnetic materials) and a AMS preconditionner.
Magnets snapping
Two magnets covered by a layer of insulator material (stiff plastic) are coming into contact with each other (snapping) due to electromagnetic forces. This example shows how magnets can be simulated using the EM solver and how dynamic motion due to magnetic forces can be simulated. It uses the FEM-BEM monolithic magnetostatics solver (used for zero-conductivity ferromagnetic materials) and a AMS preconditionner.
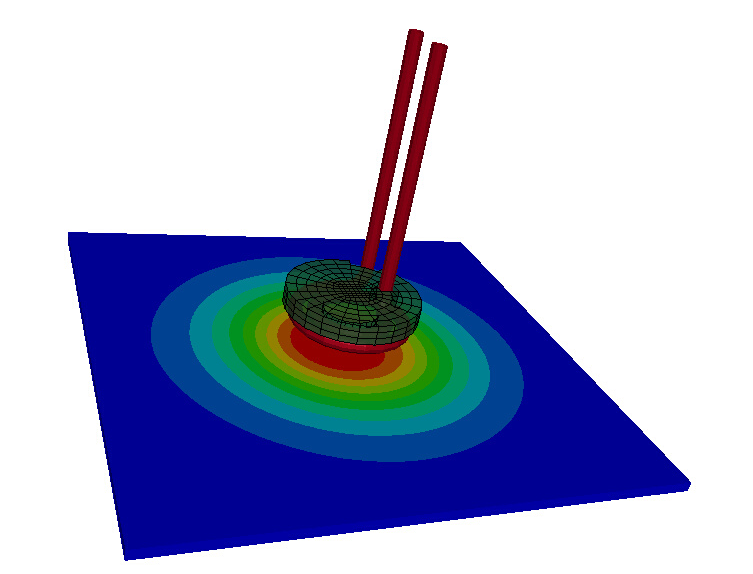
Pancake coil Inductive heating
This LS-DYNA simulation shows a simple pancake coil + flux concentrator inductive heating problem. The Monolithic solver must be turned on in order to handle the zero conductivity/high permeability properties of the flux concentrator. Its presence allows a stronger concentration of the magnetic field close to the coil and therefore will generate more heat in the workpiece.
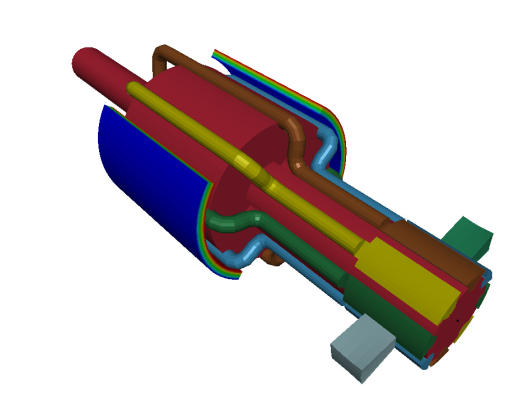
D.C Electric motor
This example shows some of the capabilities of the LS-DYNA EM solver (Post R13). Permanent magnets combined with a current carrying armature made of copper wires form an electromagnet and thus allow the simulation and study of D.C electric motors. Coupling with the structure is automatic and straightforward.
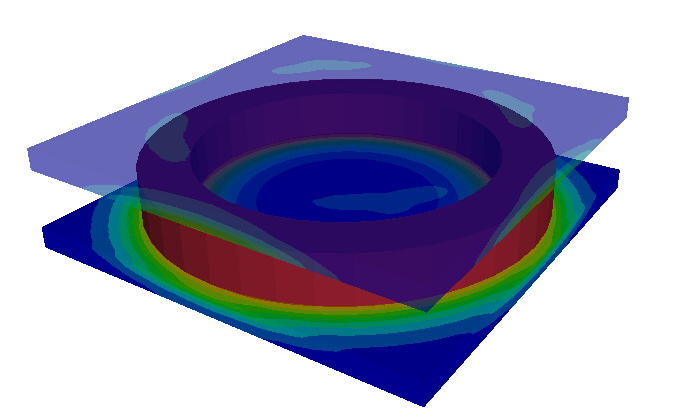
Voltage Driven Coil
This example shows a stranded coil problem that is voltage driven rather than having an imposed current. For voltage driven coils, the voltage, the number of turns as well as the coil's resistance must be provided. Since the current is an unknown, the EM material must be defined as type 2 for the coil become part of the system. This case is a validation problem first proposed by Leonard & Rodger.
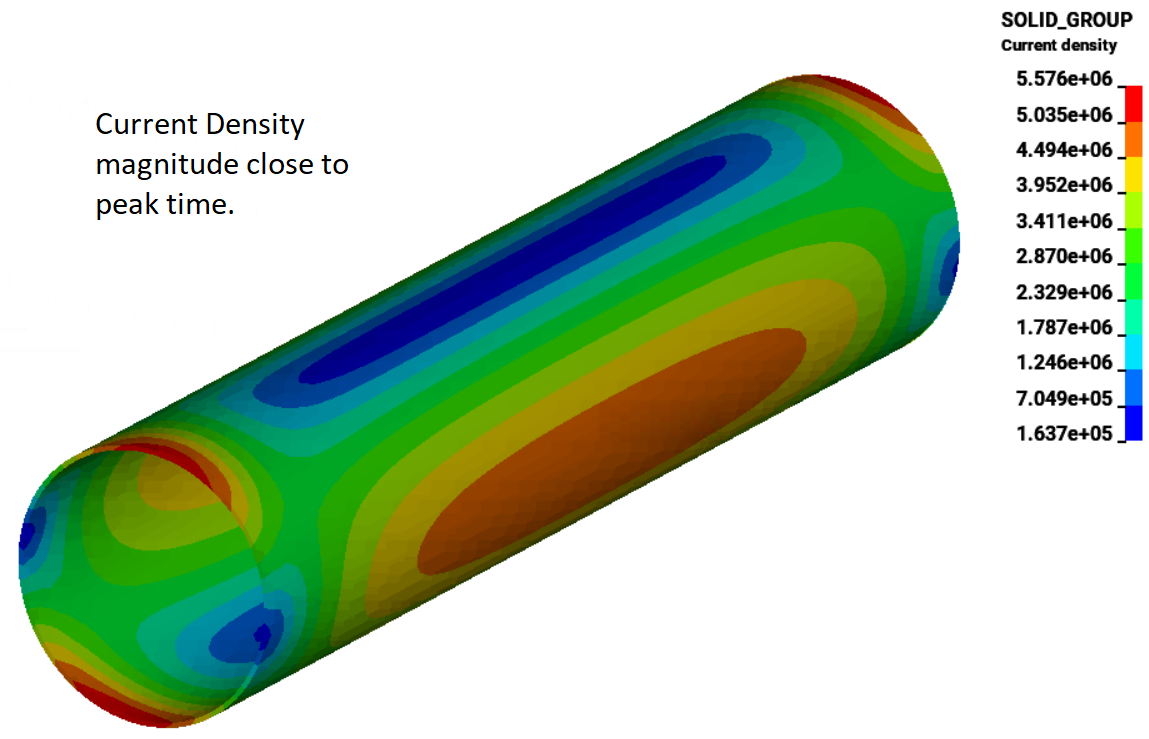
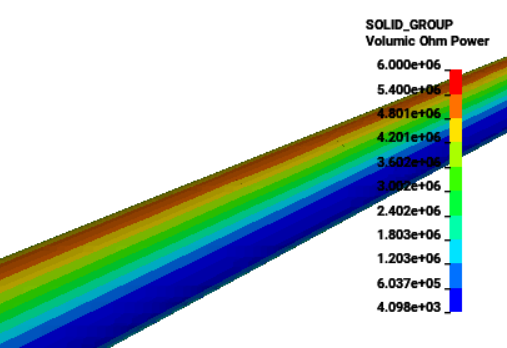
TEAM 1 problem
The TEAM 1 problem is a simple Eddy current code benchmarking problem where a conducting cylinder is placed inside a external magnetic field that decays exponentially with time. This problem is an example of using Rogowski coils and part data output. The Richardson solve or the Monolithic solve can be used and different timesteps can be selected to study the impact of stability and solution time.
TEAM 2 problem
Problem 2 of the TEAM workshops for eddy current code comparison is an infinite cylinder in a uniform magnetic field. The objective is to measure the magnetic flux amplitude and phase inside and outside the cylinder at different instants and compare to the reference solution. Thus, the Frequency Eddy current solver is used.
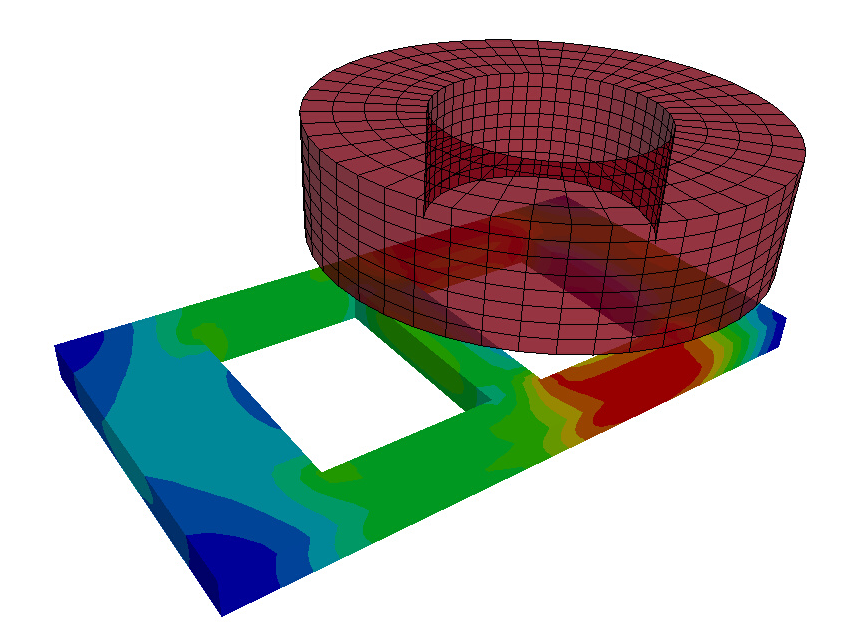
TEAM 3 problem
The TEAM 3 problem is a classic validation test case often studied and consists of a conducting ladder, having two holes with a coil above carrying a sinusoidal current. The current in the coil is considered uniform (no eddy currents) while the ladder’s induced current diffuses through its thickness (eddy currents).
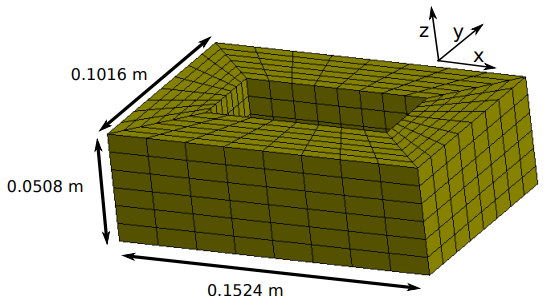
TEAM 4 problem
The TEAM 4 problem is a simple Eddy current code benchmarking problem where a solid brick is placed inside a external magnetic field that decays exponentially with time. The main objective of the problem is to calculate the total circulating current in the brick function of time.
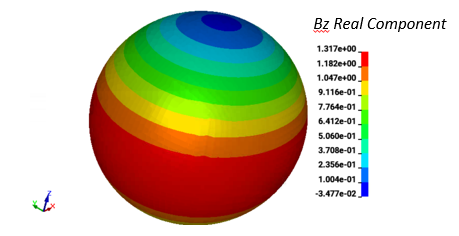
TEAM 6 problem
Problem 6 of the TEAM workshops for eddy current code comparison is a hollow conducting sphere in a uniform magnetic field. The applied field varies with time as a sinusoidal function making this problem an excellent verification case for a Frequency based Eddy current solver.
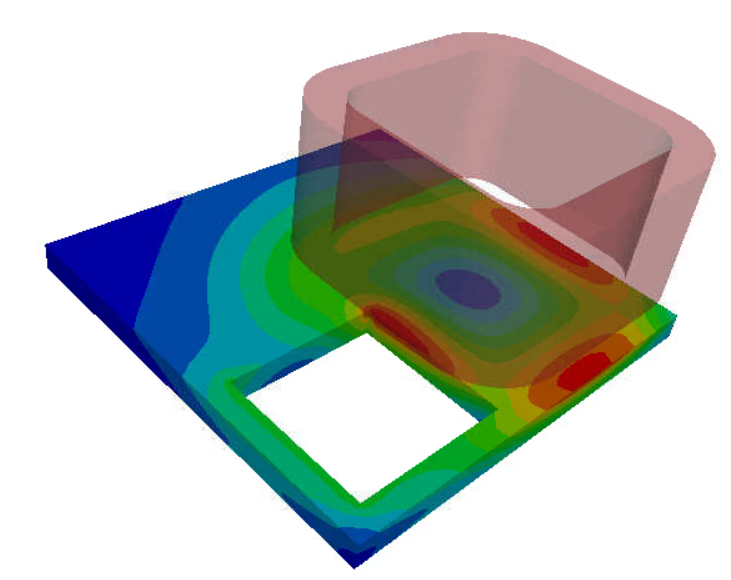
TEAM 7 problem
Problem 7 of the TEAM workshops for eddy current code comparison is a thick aluminum plate with a hole, which is placed eccentrically and set unsymmetrically in a non-uniform magnetic field. The field is produced by the exciting current which varies sinusoidally with time. The Frequency Eddy current solver is used to retrieve the Real and Imaginary parts of the Magnetic flux between the coil and plate and compare to reference results.
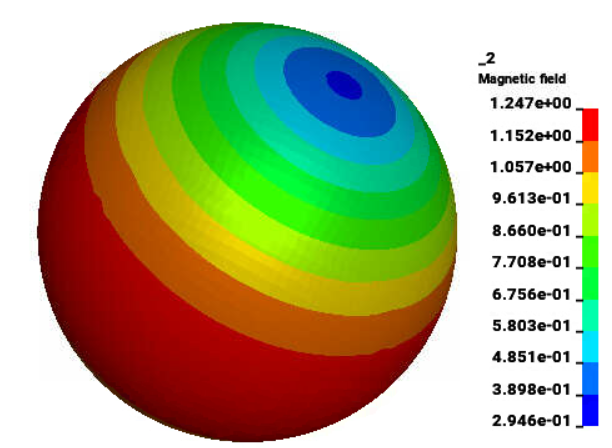
TEAM 11 problem
Problem 11 of the TEAM workshops for eddy current code comparison is a hollow conducting sphere in a uniform magnetic field. The applied field varies with time as a step function, requiring a fully transient solution. Magnetic field in and outside the sphere at different instants is measured and compared to the analytical solution.

TEAM 12 problem
The TEAM 12 features a clamped beam oscillating under the influence of an external magnetic field. Additionally, in this example, an alternative version is provided where the source of the magnetic field and therefore beam displacements is provided by a moving magnet located at the tip of the beam.

TEAM 13 problem
The TEAM 13 problem is a non linear magnetostatic case where an exciting coil with D.C current is set between two steel channels not aligned with each other and a steel plate inserted between the channels. The applied current is enough to reach steel saturation. This case is an important milestone in the validation of LS-DYNA's FEM/BEM monolithic solver for Eddy currents.
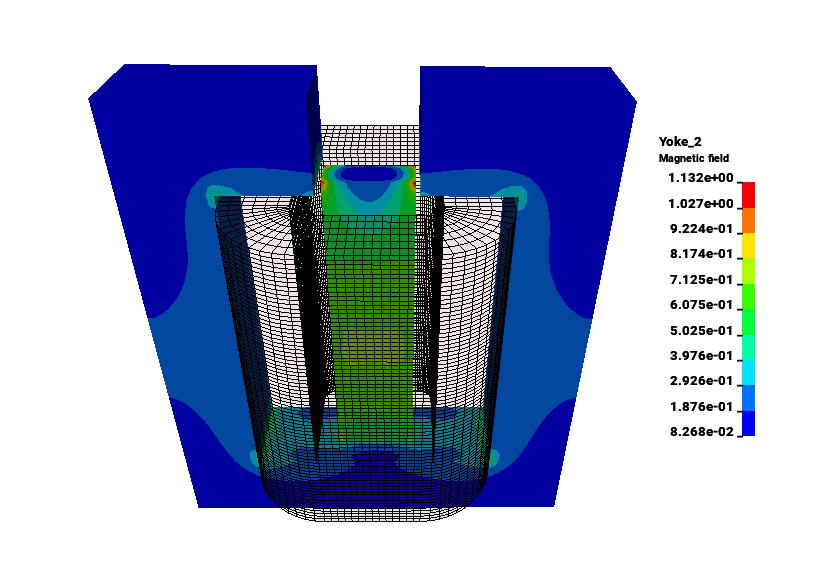
TEAM 20 problem
The TEAM 20 problem is a non linear magnetostatic 3D model for verification of magnetostatic force calculation. The center pole and yoke are made of steel and the coil is a source circuit with imposed Ampere-turns. This model allows to investigate the surface magnetic force calculation obtained by the monolithic solver in magnetostatic cases under different current excitations.
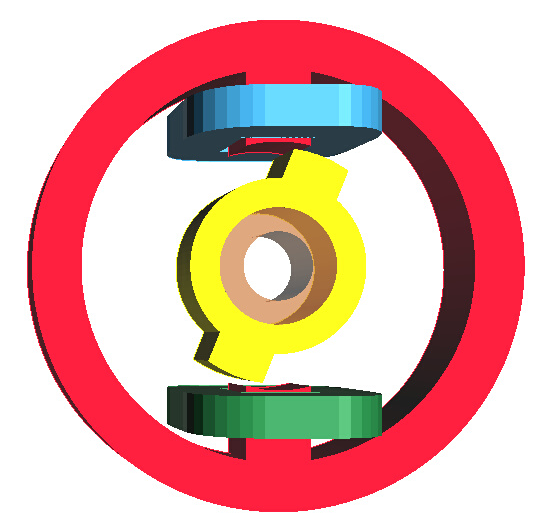
TEAM 24 Problem
The TEAM 24 workshop problem consists of a rotor mounted on a nonmagnetic stainless steel shaft and a fixed stator. The rotor is locked at a specific angle with respect to the stator. The steel magnetization curve and conductivity have been measured and are provided as input. The coils are modelled as stranded conductors with a provided voltage, resistance and number of turns. Coil current, torque, search coil flux, and Hall probe flux density are Post Treatment quantities. This input decks shows the EM monolithic solver's advanced capabilities that allow to solve non-linear time transient actuator or electric motor problems while removing the need to mesh the air
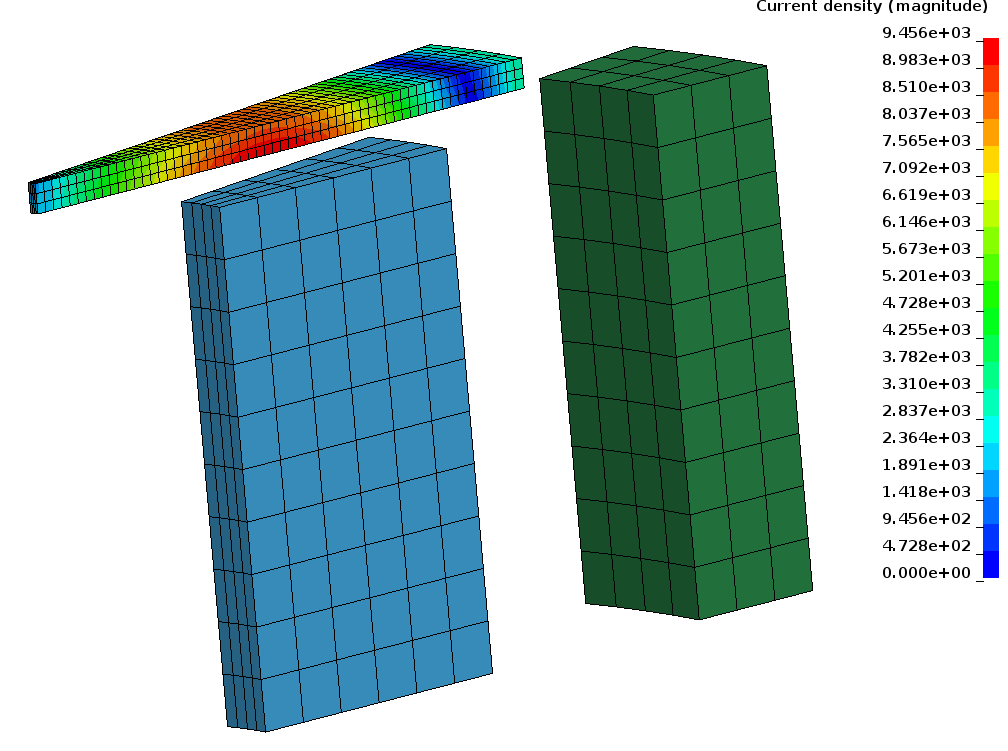
TEAM 28 Levitation problem
The TEAM 28 problem introduces an axisymmetric electrodynamic levitation device which consists of a conducting plate over two stranded coils. The aim is to determine the dynamic characteristics of the levitating plate (after some damped oscillations, the plate attains a stationary levitation height). A coupled solution of the electromagnetic and the mechanical problem is necessary.